プランニングポーカーと、「61％」の傘を着た数字の列

プランニングポーカー。面白いな、と思いつつ、どうも数字の並びが美しくない（この感覚は、特異な、個人的な感覚かもしれませんが）ので、見積もりの誤差許容という観点から、考えてみました。そもそもあれはフィボナッチ数列を1～13の範囲で示していますが、その上の20や40、あるいは下の1/2は人工的に加えています。なので以下のような、原始モデルでのフィッティングを試みています。

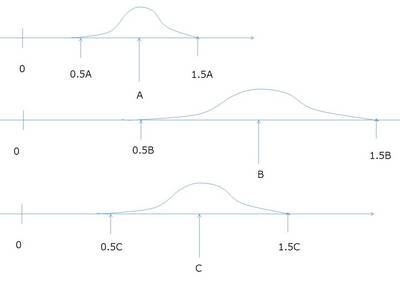
ある量を見積もる。それをAと表示する。その値は、遠くの的であれば、プラスマイナス50％の誤差を持つものだ、とプロジェクトマネージメントの入門時に学びました。Aと見積もる概算数字は、A±0.5A の傘を差したような感じのもの、というイメージがあります。

さて、数字の直線状、いくつかの数字を細かく分けてもしょせん、結構広い傘をさしているならばあまり意味がありませんで、次の大きな数字はその傘のひさしがちょうど重なればいいわけで、こんな感じになるかと思います。

１．５Aが次の数字になればいい。絵でいえばCですね。

すると、最初の点を決めると、この数字の列は出来上がります。
A　,　A×1.5　,　A×1.5×1.5　,　・・・・

下側にも行けます。下側に作るならA／1.5　,　A／（1.5×1.5）　,　・・・

これのAを、「1」でとって、入れてみるとどうだろう、というと、プランニングポーカーの並びにちょっと近い。

次にAを「3」にしてみるとどうか。この道具は、真ん中位を基準の量にして考えるので、1を基準にするより「3」の方が、より概念操作上の妥当考えられるのでは、という仮説で。

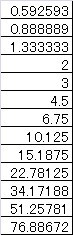
計算したところこうです。

結構いい線行きました。小数点以下を四捨五入すると、1,2,3,5,7,10,15,23、という感じで大分近い。この、1.5ファクターをもう少しだけ大きくとるとさらにフィットしそうです。大きくとる、ということは、Aの周りに着せる誤差の傘をもすこし大きくとってあげるということを意味します。

いろいろいじってみると、1.61の時がびしっと値が合いました。

これだと、四捨五入して、1,2,3,5,8,13,20,となります。なお、1.62にすると、最後が20ではなく21になってしまいます。逆に1.59にすると、13，20が12,19と小さくなります。なぜかはわかりませんが、この誤差の傘を着せて、数字の上に列を作るならば、その時の笠の広さは、Aを中心に±0．61Aという感じになります。ちょっと広めですが、ざっくり直観的に、さっと選ぶにはいいぐらいではないでしょうか。

荒っぽい原始的なモデルと、恣意的な基準点選択をしたので、議論としては、こういう風に考えてみた、レベルを全く声ない物ですが、このモデルを仮に正として残りのカードを作るならば、こうなるべきでしょう。

「0.4」「0.7」「32」「52」「84」

セットを全部書くならば

「0.4」「0.7」「1」「2」「3」「5」「8」「13」「20」「32」「52」「84」「?」（の13枚）

かと。実際には20を超えて大きな数が52か50かはさほど効かないしかえって52の様なものが精度高く考えることを強いる気がしてあまり使えない気もしますけれど。ただ、32が2の５乗であること、52が一年間の週の数であること、など、面白い数字の並びではあるなと思います。下側も、位置に満たないものが0.5であると言い切れる場合よりは、半分弱（0.4）とか、1には満たないが半分よりは多い（0.7）というのは区切り感としてはありな気もします。なお、もともとのカードセットが13枚でしたので、ゼロを省き、インフィニティ―を入れて13枚揃えにしました。