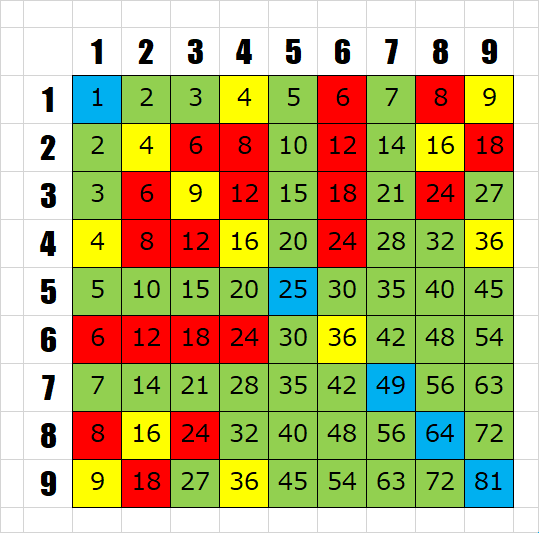
九九の答え、というのは、１～８１までの数のうち、いくつを占めるのだろう？

夕食の時に、ふと、娘のテストを見ました。小２で掛け算を習うと、今は、掛け算の順番に正解・不正解、があるというので、教科書を借りて熟読してしまいました。「１ユニットあたりの内包数」を先に書く、というルールのようで、カケルの後ろに来るのは「そのユニット数」だということでした。掛け算の順番を決めてみた、というのは、『へー、面白いことを教科書を作る人は考えたもんだ』と、ひとしきり家族で議論していました。どんな数学的な思想に基づくのか。

さて、それはさておき、教科書をみていて、ふと、興味がわきました。

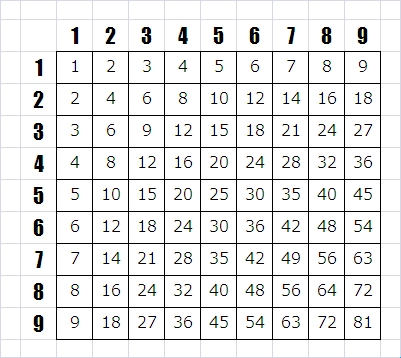
九九の答え、というのは、１～８１までの数のうち、いくつを占めるのだろう？

３×７も、７×３も、２１なので、九九の表の上には、何度も出てくる「答え」があるし、一方で５×５のような、九九の表の上で１度しか出現しないものもいくつかあります。その意味では、だいたい、１～８１の整数（８１個の整数）の半分弱、ぐらいだろうか、と見通しを立てました。

地道に数えてみると、こうなることがわかりました。

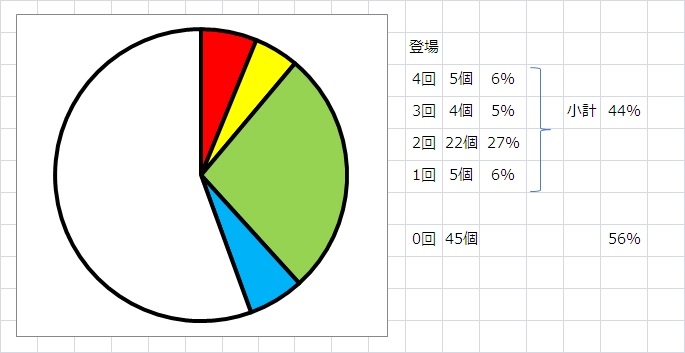
４回登場する数が「５個」ありました。
３回登場する数が「４個」ありました。
２回登場する数が「２２個」ありました。
１回登場する数が「５個」ありました。

合計で「３６個」でした。（44%）

81個の数のうち、36個しか、九九の答えとしては登場しない、というのは、「けっこう、スカスカなんだなぁ」という感じがしました。

～　そして、長い余談　～

81以下の数字で、九九の答えとしては出てこない数字はなんだろう。今度はそこに興味がいきました。（直感的に考えたのは”出てこない数は素数でしょ？”と。もちろん、答えの一部ではあるのですが、100以下の素数は25個しかないので、素数以外の数字で、九九の答えにならない数があるはずだな、と思いました。

そこで、少し、色を付けてプロットしてみました（赤、黄、緑、青＝4回、3回、2回、1回、です。ヒートマップ的に、多いほど、あったかい色にしてあります）。

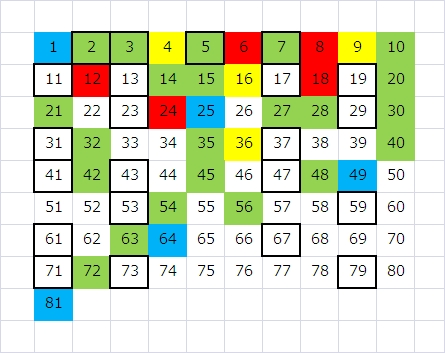
こうしてみると、後ろの方がスカスカです。

（ 素数以外でまず出現するのは、22、とか、26、といった、2×11、2×13、のような、二けたの素数との積です。）

なにか、見せ方を変えると、出現する場所に法則性を感じられるのではないかと思い、いくつかの表現をしてみます。

先ず、81個＝9の二乗、なので、9×9の配置にしてみます。

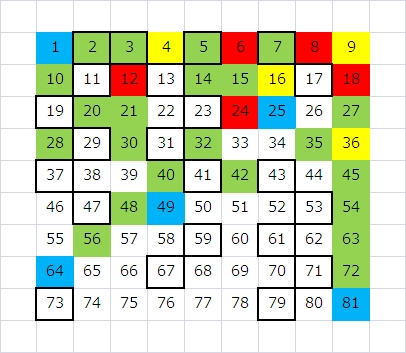
すこし、散らばり方に傾向が見えるような気もします。

すこし見方を変えてみます。
最も沢山出現する「4回（赤いマス）」について。

これは、どうも、「2」や「3」というとても小さい素数だけに約分される数で、直観的に「6進数」で書くと、何かすっきりしそうな気がしました。なので、6で折り返すようにしてみます。

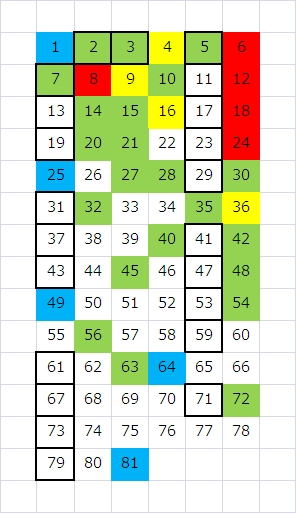
こんな感じです。8だけは、この系統ではないなぁ、という分かったような分からないような感じの感想です。

それから、1度しか出現しないもの（青いマス）と、3度出現するもの（黄色いマス）、というものは、九九の表の対角線上（同じ数をかけている所）と強く関係しているはずだ、思いましたので、少し変わった書き方をしてみました。整数の二乗になるところで折り返すという書き方です。

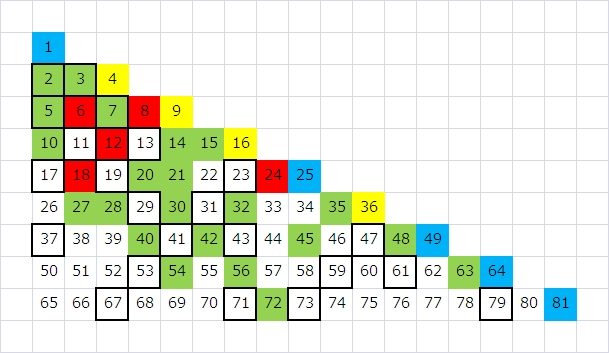
1回（青色）と3回（黄色）は、右端（つまり、整数の二乗の数）にだけあることがわかります。

もっと、シンプルに、一直線に並べてみたら、何か印象があるんじゃないだろうか、とも思って作ってみました。

うーむ、・・・さほど、想起できるものが無いように思います。

そんな感じで長い余談を終わります。

最後に、九九の表そのものに、出現回数の色を付けてみたものを載せておきます。

（ 遠目に見ると、「インベーダーに出てくる、上の方の高得点な敵」か「チューリップ」のように見えなくもないですが、だから、どうした、ということはないのですが。 ）

※上図の色の塗間違いがありまして、修正しました。